Polyphase FIR Filter Downsampling

This is a long-delayed post. As a father of two, who is living in one of the most expensive cities in the world, life is full of challenges. In most cases, after decomposition, they always go down to two reasons: the lack of money and/or time. It’s a simple truth, but I took years to realize it. Many years ago when I started writing DSP code, all I cared about was the correctness. My code used to have no readability, no structure, and no efficiency. Especially, when using Matlab, I used to pay no attention to the memory or CPU resource allocation, unless it is a heavy task or is going to be implemented on the hardware.

Therefore, I want to write a series of posts on how to efficiently implement some DSP algorithms. I am going to start with the polyphase FIR filter downsampling.

Conventional downsampling

Downsampling normally means reducing the sampling rate of a given digital signal by an integer factor $M$. According to the sampling theorem, we can not downsample a signal simply by keeping every Mth sample. Otherwise, there will be aliasing, or in other words, high-frequency components will be mixed into the downsampling output. Therefore, before decimation, a low pass filter (anti-aliasing filter) is required to remove the high-frequency components.

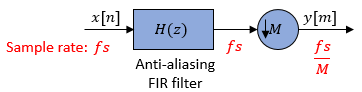
The anti-aliasing filter is normally an FIR filter. If the length of the filter is fir_len, to output one sample, we will need fir_len multiplications. The multiplication cannot be shared between samples, so if the length of the signal is sig_len, it requires fir_len * sig_len multiplications. However, after decimation, only sig_len / M samples are left, which means, the effective number of multiplications is fir_len * sig_len / M, and other multiplications are wasted.

Polyphase FIR filter downsampling

The most interesting part of polyphase FIR filter downsampling is that it downsamples the signal first and then does the filtering, such that the multiplications are applied only to the leftover samples.

As always, Matlab has a document to explain this algorithm. This reversed order of downsampling (or upsampling) and filtering is called multirate noble identity. I am not going to past all the equations and plots here, but to explain the idea.

The polyphase FIR filter downsampling is a new structure. It is a decimator that is implemented using a polyphase filter. The first step of downsampling is to split the signal into $M$ sub-signals, and each sub-signal is a downsampled version of the original signal, so there is no sample discarded as the conventional downsampling. The second step is to filter each sub-signal with a sub-filter. Just like the sub-signals, the sub-filters are downsampled versions of the original low-pass FIR filter. The initial sample (or phase) when downsampling the low-pass filter is different for each sub-filter. That is why the sub-filters are called polyphase filters.

Illustration and demo code

There is an example of a polyphase FIR filter downsampling in the following figure, where the signal is downsampled by a factor of $M = 3$. The impulse response of the low-pass FIR filter is $h$, and for demonstration purposes, its length fir_len is set to 6. The input signal $x$ is split by a commutator switch as shown below.

The demo code is as follows. The input signal $x$ and the impulse response $h$ are defined for demonstration purposes. dsp.FIRDecimator is a Matlab built-in object that implements the polyphase FIR filter downsampling. We can see that our output y_polyphase is the same as the reference output y_ref.

x = (0:11)';
M = 3;
h = (0:5)';
% use Matlab built-in function
firdecim = dsp.FIRDecimator(M,h);
y_ref = firdecim(x);

fir_len = length(h);
% if the fir_len is not intger multiple of fir_len, padding zeros
if (rem(fir_len, M) ~= 0)
     nzeros = M - rem(fir_len, M);
     h = [h; zeros(nzeros,1)];  
end
len = length(h);
ncolm = len / M;

polyphase_filt = flipud(reshape(h, M, ncolm));

% init output
nx = length(x);
y_polyphase = zeros(floor((nx-1)/M)+1,1);
y_polyphase(1) = x(1) * polyphase_filt(end, 1);

% init filter register to store x
filt_reg = zeros(size(polyphase_filt));
filt_reg(end,2) = x(1);

for idx = 2:length(y_polyphase)
    xst = (idx-2) * M + 2;
    filt_reg(:,1) = x(xst:xst+M-1);
    y_polyphase(idx) = sum(polyphase_filt .* filt_reg, 'all');
    filt_reg = circshift(filt_reg,1,2);
end

That is all for this post. Hope you enjoy it.